Electricity Generation Forecast using ANN with R, Dr. Arunachalam Rajagopal

Electricity Generation Forecast using Artificial Neural Network with R 

Arunachalam Rajagopal

The artificial neural network (ANN) is based on the concept of machine learning. ANN attempts to mimic the human brain into the machine (computer). ANNs attempt to learn the patterns that are exhibited in the training dataset (input - independent variable and output - dependent variable). Then based on the previous learning, ANN attempts to give generalized solution for the total dataset. The solution could be forecast in a time series dataset or causal regression model. It could also be used for classification of the dataset like what is done in a discriminant analysis or logistic regression.

Artificial neural network (ANN) are data-driven and self-adaptive. There is no need to make any a priori assumption on the input data. The neural network model is formed in an adaptive manner based on the pattern exhibited by the dataset. The artificial neural network is basically non-linear in contrasts to the linear regression models including ARIMA models. This makes it more adaptive to different kinds of dataset and the predictions are mostly more accurate than the other models of forecasting or classification models

ANN Architecture:

The most widely used ANN architecture is based on multilayer perceptron (MLP). MLP in general comprises of input layer, single hidden layer, and output layer. There could also be more than one hidden layer also. The nodes in the various layers are known as processing elements. The elements in the input, hidden, and output layers are connected by acyclic links. Each link is associated with a weight. The most commonly used ANN architecture consists of three layers: input layer, a single hidden layer, and an output layer. The network works on the principle of feed forward network (FNN) mechanism.

Yk = pi_out (alpha_k + sum over h (Whk * pi_h ( alpha_h + sum over i ( Wih * Xi))))

where,

W = weight associated with each link in the network

i = number of inputs

h = number of elements in the hidden layer

k = number of outputs

The activation function pi_h of the hidden layer is taken to be logistic function; pi_out is activation function at the output level; alpha_h and alpha_k are bias coefficients.

f(z) = exp(z)/(1 + exp(z))

A) Electricity generation forecasting:

The dataset for forecasting comprises of data starting from 1960-61 to 2018-19. The response variable is electricity generated in billion units (billion kwh). The regressor or the independent variables are gdp in billions of rupees and population in million. The following R-code has been made use of making forecast of electricity generation in billion kwh for the next 10 years. The neural network diagram has been plotted using 'NeuralNetTools' package and is shown in Figure 1. The file ‘bnkwh_gdp.csv’ holds the dataset for this example.

> #R code:

> abc <- read.csv("bnkwh_gdp.csv", sep=",", header=TRUE)

> head(abc)

     year pop_mn gdp_bn gdp_pcap bn_kwh

1 1960-61    434 178.70   411.75  16.94

2 1961-62    444 189.12   425.95  20.15

3 1962-63    454 203.21   447.60  23.36

4 1963-64    464 233.50   503.23  26.57

5 1964-65    474 272.22   574.30  29.78

6 1965-66    485 286.93   591.61  32.99

> kwhgdp<-data.frame(abc[,c(2,3,5)])

> kwhgdp

	pop_mn	gdp_bn	bn_kwh
1	434	178.70	16.94
2	444	189.12	20.15
3	454	203.21	23.36
4	464	233.50	26.57
5	474	272.22	29.78
6	485	286.93	32.99
7	495	324.39	37.81
8	506	380.03	42.62
9	518	402.57	47.43
10	529	443.34	51.62
11	541	473.54	55.80
12	554	507.08	59.43
13	567	559.12	63.06
14	580	680.95	66.69
15	593	804.79	72.94
16	607	864.52	79.20
17	620	931.89	85.30
18	634	1056.15	91.40
19	648	1144.91	102.52
20	664	1258.82	104.70
21	679	1499.87	120.80
22	692	1758.45	122.10
23	708	1960.10	130.30
24	723	2280.77	140.20
25	739	2551.87	156.86
26	755	2880.95	170.40
27	771	3221.44	187.70
28	788	3655.92	202.10
29	805	4323.97	221.40
30	822	4961.97	245.44
31	839	5786.67	264.30
32	856	6637.98	287.03
33	872	7629.00	301.40
34	892	8792.75	324.00
35	910	10325.07	350.40
36	928	12132.41	380.00
37	946	14061.95	395.89
38	964	15591.89	421.70
39	983	17884.10	448.50
40	1001	20076.99	480.70
41	1019	21546.80	499.50
42	1040	23357.77	517.44
43	1056	25196.37	532.70
44	1072	28207.95	565.10
45	1089	32198.35	594.40
46	1106	36672.53	623.80
47	1122	42614.72	670.65
48	1138	49665.78	723.00
49	1154	55971.40	741.20
50	1170	64398.27	799.80
51	1186	77023.08	844.80
52	1202	89328.92	923.20
53	1217	98345.81	964.50
54	1239	111328.77	1014.80
55	1254	123407.72	1048.40
56	1324	135226.56	1090.85
57	1350	149941.09	1135.33
58	1354	166275.85	1206.31
59	1369	190100.00	1249.34

> scalemin<-apply(kwhgdp,2,min)

> scalemax<-apply(kwhgdp,2,max)

> scaledata<-data.frame(scale(kwhgdp, center=scalemin, scale=scalemax-scalemin))

> scaledata

	pop_mn	gdp_bn	bn_kwh
1	0.000000000	0.000000000	0.000000000
2	0.010695190	0.000054865	0.002604674
3	0.021390370	0.000129054	0.005209348
4	0.032085560	0.000288541	0.007814021
5	0.042780750	0.000492415	0.010418695
6	0.054545450	0.000569868	0.013023369
7	0.065240640	0.000767107	0.016934437
8	0.077005350	0.001060071	0.020837390
9	0.089839570	0.001178751	0.024740344
10	0.101604280	0.001393419	0.028140214
11	0.114438500	0.001552433	0.031531970
12	0.128342250	0.001729032	0.034477442
13	0.142245990	0.002003040	0.037422915
14	0.156149730	0.002644516	0.040368387
15	0.170053480	0.003296576	0.045439792
16	0.185026740	0.003611075	0.050519312
17	0.198930480	0.003965801	0.055469004
18	0.213903740	0.004620072	0.060418695
19	0.228877010	0.005087423	0.069441740
20	0.245989300	0.005687198	0.071210646
21	0.262032090	0.006956408	0.084274586
22	0.275935830	0.008317919	0.085329438
23	0.293048130	0.009379675	0.091983122
24	0.309090910	0.011068110	0.100016228
25	0.326203210	0.012495540	0.113534567
26	0.343315510	0.014228260	0.124521259
27	0.360427810	0.016021060	0.138558909
28	0.378609630	0.018308740	0.150243427
29	0.396791440	0.021826250	0.165903927
30	0.414973260	0.025185540	0.185410581
31	0.433155080	0.029527860	0.200714054
32	0.451336900	0.034010300	0.219157741
33	0.468449200	0.039228350	0.230817916
34	0.489839570	0.045355890	0.249156118
35	0.509090910	0.053424080	0.270577735
36	0.528342250	0.062940330	0.294595910
37	0.547593580	0.073100020	0.307489451
38	0.566844920	0.081155670	0.328432327
39	0.587165780	0.093224930	0.350178513
40	0.606417110	0.104771200	0.376306394
41	0.625668450	0.112510300	0.391561181
42	0.648128340	0.122045700	0.406118143
43	0.665240640	0.131726500	0.418500487
44	0.682352940	0.147583500	0.444790652
45	0.700534760	0.168594300	0.468565401
46	0.718716580	0.192152400	0.492421292
47	0.735828880	0.223440000	0.530436547
48	0.752941180	0.260566200	0.572914638
49	0.770053480	0.293767500	0.587682571
50	0.787165780	0.338137800	0.635232068
51	0.804278070	0.404611700	0.671746186
52	0.821390370	0.469406100	0.735361895
53	0.837433160	0.516883100	0.768873742
54	0.860962570	0.585242800	0.809688413
55	0.877005350	0.648842500	0.836952288
56	0.951871660	0.711072700	0.871397274
57	0.979679140	0.788549700	0.907489451
58	0.983957220	0.874557800	0.965084388
59	1.000000000	1.000000000	1.000000000

> set.seed(123)

> library(nnet)

> library(NeuralNetTools)

> kwh_nn <- nnet(bn_kwh ~ gdp_bn + pop_mn, scaledata, size = 5, decay = 1e-3, linout = T, skip = F, maxit = 1000, Hess = T)

# weights:  21

initial  value 7.652763

iter  10 value 0.029795

iter  20 value 0.026070

iter  30 value 0.024238

iter  40 value 0.023878

iter  50 value 0.023284

iter  60 value 0.022457

……………………………………

iter 250 value 0.019137

iter 260 value 0.019133

iter 270 value 0.019133

iter 280 value 0.019132

iter 290 value 0.019132

iter 300 value 0.019132

final  value 0.019132

converged

> summary(kwh_nn)

a 2-5-1 network with 21 weights

options were - linear output units  decay=0.001

 b->h1 i1->h1 i2->h1

  0.02   0.12  -0.16

 b->h2 i1->h2 i2->h2

  1.41  -1.53  -2.24

 b->h3 i1->h3 i2->h3

  0.02   0.12  -0.16

 b->h4 i1->h4 i2->h4

 -0.19   0.43  -1.02

 b->h5 i1->h5 i2->h5

  0.02   0.12  -0.16

 b->o h1->o h2->o h3->o h4->o h5->o

 0.35  0.31 -1.62  0.31  1.05  0.31

> plotnet(kwh_nn)

> ycap <- fitted.values(kwh_nn)*(max(kwhgdp$bn_kwh)-min(kwhgdp$bn_kwh))+min(kwhgdp$bn_kwh)

> bnkwh<-data.frame(actualbnkwh=kwhgdp$bn_kwh, fittedbnkwh=ycap[,1])

 Figure 1 Neural network diagram

> bnkwh

	actualbnkwh	fittedbnkwh
1	16.94	4.92
2	20.15	8.53
3	23.36	12.26
4	26.57	16.17
5	29.78	20.22
6	32.99	24.71
7	37.81	29.01
8	42.62	33.92
9	47.43	39.29
10	51.62	44.45
11	55.80	50.17
12	59.43	56.57
13	63.06	63.23
14	66.69	70.37
15	72.94	77.71
16	79.20	85.55
17	85.30	93.07
18	91.40	101.60
19	102.52	110.20
20	104.70	120.35
21	120.80	130.69
22	122.10	140.08
23	130.30	151.37
24	140.20	162.79
25	156.86	174.92
26	170.40	187.56
27	187.70	200.51
28	202.10	214.87
29	221.40	230.57
30	245.44	246.40
31	264.30	263.36
32	287.03	280.68
33	301.40	298.08
34	324.00	319.73
35	350.40	341.75
36	380.00	365.27
37	395.89	389.52
38	421.70	411.92
39	448.50	438.89
40	480.70	464.53
41	499.50	486.61
42	517.44	512.71
43	532.70	534.66
44	565.10	561.97
45	594.40	594.35
46	623.80	628.45
47	670.65	667.76
48	723.00	711.02
49	741.20	749.76
50	799.80	796.10
51	844.80	857.26
52	923.20	913.66
53	964.50	954.29
54	1014.80	1008.98
55	1048.40	1053.77
56	1090.85	1108.56
57	1135.33	1152.28
58	1206.31	1192.35
59	1249.34	1245.93

> plot(bnkwh$actualbnkwh,bnkwh$fittedbnkwh, xlab="actual bnkwh", ylab="fitted bnkwh", type="p", pch=20, col=4)

> abline(0,1, col=2)

Figure 2 actual vs fitted bnkwh

> rmse<-sqrt(sum((bnkwh$actual-bnkwh$fitted)^2)/nrow(bnkwh))

> rmse

[1] 10.47169

The actual bnkwh versus predicted bnkwh scatter has been plotted in order to understand the model fit. The scatter plot has been shown in Figure 2.

The forecast has been done for bnkwh for the next 10 years. The new data for regressor variables has been estimated by making use of arima model. In fact, auto.arima function of the 'forecast' package has been used for making the estimation of gross domestic product in billion rupees and population in million.

> #arima prediction of 'popmn' for next ten years

> library(forecast)

> auto.arima(scaledata$pop_mn)

Series: scaledata$pop_mn

ARIMA(0,2,1)

Coefficients:

          ma1

      -0.8907

s.e.   0.0551

sigma^2 estimated as 7.012e-05:  log likelihood=191.45

AIC=-378.89   AICc=-378.67   BIC=-374.81

> fit2<-arima(scaledata$pop_mn, order=c(0,2,1))

> fit2

Call:

arima(x = scaledata$pop_mn, order = c(0, 2, 1))

Coefficients:

          ma1

      -0.8907

s.e.   0.0551

sigma^2 estimated as 6.889e-05:  log likelihood = 191.45,  aic = -378.89

> fpre2<-predict(fit2, n.ahead=10)

> fprepopmn<-fpre2$pred

> fprepopmn

Time Series:

Start = 60

End = 69

Frequency = 1

 [1] 1.021688 1.043377 1.065065 1.086754 1.108442 1.130131 1.151819 1.173508

 [9] 1.195196 1.216885

> #arima prediction of 'gdpbn' for next ten years

> library(forecast)

> auto.arima(scaledata$gdp_bn)

Series: scaledata$gdp_bn

ARIMA(1,2,1)

Coefficients:

           ar1        ma1

         0.9820  -0.8670

s.e.  0.0287   0.0836

sigma^2 estimated as 5.574e-05:  log likelihood=198.83

AIC=-391.67   AICc=-391.22   BIC=-385.54

> fit3<-arima(scaledata$gdp_bn, order=c(1,2,1))

> fit3

Call:

arima(x = scaledata$gdp_bn, order = c(1, 2, 1))

Coefficients:

           ar1        ma1

         0.9820  -0.8670

s.e.  0.0287   0.0836

sigma^2 estimated as 5.378e-05:  log likelihood = 198.83,  aic = -391.67

> fpre3<-predict(fit3, n.ahead=10)

> fpregdpbn<-fpre3$pred

> fpregdpbn

Time Series:

Start = 60

End = 69

Frequency = 1

 [1] 1.133588 1.275175 1.424617 1.581772 1.746503 1.918672 2.098146 2.284793

 [9] 2.478485 2.679094

> futuredf<-data.frame(pop_mn=fprepopmn, gdp_bn=fpregdpbn)

> futbnkwh<-predict(kwh_nn,futuredf)

> bnkwhfuture<-futbnkwh*(max(kwhgdp$bn_kwh)-min(kwhgdp$bn_kwh))+min(kwhgdp$bn_kwh)

> bnkwhfuture

       [,1]

1  1295.468

2  1340.575

3  1381.663

4  1419.304

5  1454.158

6  1486.896

7  1518.160

8  1548.522

9  1578.469

10 1608.398

> fittedbnkwh<-ts(bnkwh$fittedbnkwh,start=1)

> futurebnkwh<-ts(bnkwhfuture,start=60)

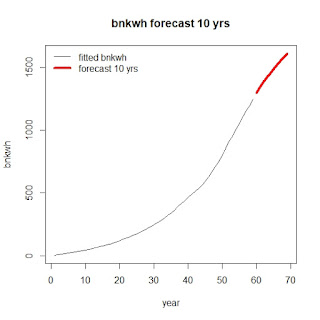
> ts.plot(fittedbnkwh, futurebnkwh, type="l", col=c(1,2), lwd=c(1,4), xlab="year", ylab="bnkwh", main="bnkwh forecast 10 yrs")

> legend("topleft", lty=c(1,1), col=c(1,2), lwd=c(1,4), legend=c("fitted bnkwh","forecast 10 yrs"),bty="n")

Figure 3 forecast of bnkwh for  next 10 years

 #Leave-one-out cross validation method:

> #R code:

> abc <- read.csv("bnkwh_gdp.csv", sep=",", header=TRUE)

> kwhgdp<-data.frame(abc[,c(2,3,5)])

> scalemin<-apply(kwhgdp,2,min)

> scalemax<-apply(kwhgdp,2,max)

> scaledata<-data.frame(scale(kwhgdp, center=scalemin, scale=scalemax-scalemin))

> scaledata

	pop_mn	gdp_bn	bn_kwh
1	0.000000000	0.000000000	0.000000000
2	0.010695190	0.000054865	0.002604674
3	0.021390370	0.000129054	0.005209348
4	0.032085560	0.000288541	0.007814021
5	0.042780750	0.000492415	0.010418695
6	0.054545450	0.000569868	0.013023369
7	0.065240640	0.000767107	0.016934437
8	0.077005350	0.001060071	0.020837390
9	0.089839570	0.001178751	0.024740344
10	0.101604280	0.001393419	0.028140214
11	0.114438500	0.001552433	0.031531970
12	0.128342250	0.001729032	0.034477442
13	0.142245990	0.002003040	0.037422915
14	0.156149730	0.002644516	0.040368387
15	0.170053480	0.003296576	0.045439792
16	0.185026740	0.003611075	0.050519312
17	0.198930480	0.003965801	0.055469004
18	0.213903740	0.004620072	0.060418695
19	0.228877010	0.005087423	0.069441740
20	0.245989300	0.005687198	0.071210646
21	0.262032090	0.006956408	0.084274586
22	0.275935830	0.008317919	0.085329438
23	0.293048130	0.009379675	0.091983122
24	0.309090910	0.011068110	0.100016228
25	0.326203210	0.012495540	0.113534567
26	0.343315510	0.014228260	0.124521259
27	0.360427810	0.016021060	0.138558909
28	0.378609630	0.018308740	0.150243427
29	0.396791440	0.021826250	0.165903927
30	0.414973260	0.025185540	0.185410581
31	0.433155080	0.029527860	0.200714054
32	0.451336900	0.034010300	0.219157741
33	0.468449200	0.039228350	0.230817916
34	0.489839570	0.045355890	0.249156118
35	0.509090910	0.053424080	0.270577735
36	0.528342250	0.062940330	0.294595910
37	0.547593580	0.073100020	0.307489451
38	0.566844920	0.081155670	0.328432327
39	0.587165780	0.093224930	0.350178513
40	0.606417110	0.104771200	0.376306394
41	0.625668450	0.112510300	0.391561181
42	0.648128340	0.122045700	0.406118143
43	0.665240640	0.131726500	0.418500487
44	0.682352940	0.147583500	0.444790652
45	0.700534760	0.168594300	0.468565401
46	0.718716580	0.192152400	0.492421292
47	0.735828880	0.223440000	0.530436547
48	0.752941180	0.260566200	0.572914638
49	0.770053480	0.293767500	0.587682571
50	0.787165780	0.338137800	0.635232068
51	0.804278070	0.404611700	0.671746186
52	0.821390370	0.469406100	0.735361895
53	0.837433160	0.516883100	0.768873742
54	0.860962570	0.585242800	0.809688413
55	0.877005350	0.648842500	0.836952288
56	0.951871660	0.711072700	0.871397274
57	0.979679140	0.788549700	0.907489451
58	0.983957220	0.874557800	0.965084388
59	1.000000000	1.000000000	1.000000000

> nnpredlevel<-numeric(nrow(kwhgdp))

> i<-integer(nrow(kwhgdp))

> xyz<-numeric(nrow(kwhgdp))

> library(nnet)

> for (j in 1:5){

+ for (i in 1:nrow(kwhgdp)) {

+ nntest<-as.data.frame(scaledata[i,c(1:2)]);

+ nntrain<-as.data.frame(scaledata[-i,]);

+ nnfit<-nnet(bn_kwh~gdp_bn+pop_mn, data=nntrain, size = 4, decay = 1e-3, linout = T, skip = F, maxit = 1000, Hess = T);

+ nnpred<-predict(nnfit, nntest);

+ nnpredlevel[i]<-nnpred[,1]*(max(kwhgdp$bn_kwh)-min(kwhgdp$bn_kwh))+min(kwhgdp$bn_kwh);

+ }

+ nnpredlevel

+ xyz<-cbind(xyz,nnpredlevel)

+ }

# weights:  17

initial  value 6.315430

iter  10 value 0.043400

iter  20 value 0.029248

iter  30 value 0.026542

iter  40 value 0.025696

iter  50 value 0.024177

iter  60 value 0.022226

iter  70 value 0.021287

iter  80 value 0.020766

iter  90 value 0.020102

iter 100 value 0.019594

iter 110 value 0.019382

iter 120 value 0.019246

iter 130 value 0.019207

iter 140 value 0.019160

final  value 0.019156

converged

........................

........................

# weights:  17

initial  value 5.533753

iter  10 value 0.041560

iter  20 value 0.027292

iter  30 value 0.022990

iter  40 value 0.022279

iter  50 value 0.020596

iter  60 value 0.020322

iter  70 value 0.020144

iter  80 value 0.019869

iter  90 value 0.019411

iter 100 value 0.019302

iter 110 value 0.019168

iter 120 value 0.019069

iter 130 value 0.019016

iter 140 value 0.018898

iter 150 value 0.018871

iter 160 value 0.018856

iter 170 value 0.018841

iter 180 value 0.018836

iter 190 value 0.018836

iter 200 value 0.018835

iter 210 value 0.018835

iter 210 value 0.018835

iter 210 value 0.018835

final  value 0.018835

converged

> xyz<-xyz[,-1]

> xyz

	nnpredlevel	nnpredlevel	nnpredlevel	nnpredlevel	nnpredlevel
[1,]	1.58957	1.55163	2.56679	2.30885	2.30784
[2,]	6.43988	6.62874	6.62314	6.62513	6.64721
[3,]	9.71847	10.62948	10.74662	9.69312	9.61503
[4,]	14.82322	15.00188	14.99733	15.01592	15.00666
[5,]	19.07408	19.18885	18.90062	19.15793	19.33661
[6,]	23.94919	23.96592	23.97387	24.08500	24.07630
[7,]	28.18760	28.15781	28.46859	28.31568	28.27585
[8,]	33.44738	33.44921	33.00205	33.44350	33.44299
[9,]	38.92595	38.83271	38.92320	38.82727	38.74279
[10,]	44.06365	43.88326	43.88333	44.08312	44.16110
[11,]	49.91590	49.91425	49.91044	49.98102	49.91191
[12,]	56.46960	56.43642	56.50409	56.41474	56.45001
[13,]	63.29158	63.25680	63.29091	63.28935	63.28870
[14,]	70.53290	70.62891	70.56593	70.56338	70.53200
[15,]	77.95662	77.92560	77.95076	77.95345	77.93343
[16,]	85.84820	85.85527	85.85935	85.87881	85.85206
[17,]	93.45821	93.44594	93.45316	93.46559	93.46716
[18,]	102.11145	102.10886	102.11007	102.54864	102.14915
[19,]	110.59833	110.59555	110.59997	110.56891	110.59417
[20,]	121.23660	121.61360	121.70392	121.27454	121.70670
[21,]	131.24988	131.21871	131.31531	131.73250	131.35157
[22,]	141.10263	141.21363	141.09433	141.07734	141.21715
[23,]	152.73168	152.63379	152.61030	152.73015	152.77698
[24,]	164.26882	164.12910	164.29025	164.11859	164.27865
[25,]	176.08491	175.95818	175.94175	175.95531	175.96007
[26,]	188.53274	188.50408	188.52275	188.50122	189.16077
[27,]	201.17042	201.17659	201.23813	201.19003	201.16410
[28,]	215.64350	216.22863	216.16810	215.48488	215.66654
[29,]	231.07762	231.61952	230.95694	231.55786	230.97177
[30,]	246.67414	246.32361	246.47803	246.46893	246.29091
[31,]	263.32476	263.16945	263.69472	263.16948	263.33151
[32,]	280.76281	280.36990	280.20359	280.74955	280.75567
[33,]	297.93349	298.21802	297.75515	297.93394	297.94592
[34,]	319.35426	319.35965	319.35887	319.52706	319.52437
[35,]	341.28680	341.14967	341.33656	341.33260	341.27332
[36,]	364.54507	364.34365	364.55115	364.34425	364.55196
[37,]	388.97786	389.18608	388.98846	389.21046	389.11537
[38,]	411.38960	411.34063	411.38285	411.38978	411.19927
[39,]	438.30897	438.17416	438.33524	438.33485	438.30050
[40,]	463.39167	463.51106	463.47021	463.50214	463.50851
[41,]	485.63055	485.65473	485.65733	485.64532	485.37044
[42,]	512.41138	512.24379	512.42736	512.37029	512.41245
[43,]	534.79987	535.09469	534.48602	534.83334	535.11134
[44,]	561.59164	561.82022	561.96304	561.23602	561.57539
[45,]	594.68838	594.53861	594.46595	594.30110	594.28840
[46,]	629.28624	628.83513	629.28136	628.85261	629.29305
[47,]	667.45192	667.47399	667.83344	667.46820	667.44984
[48,]	710.24060	709.96835	710.22699	710.24750	709.63679
[49,]	750.78032	750.77388	750.50283	750.54439	750.24516
[50,]	795.71646	795.72035	795.71928	795.68897	795.71289
[51,]	858.99474	859.05731	858.85386	859.01969	858.85236
[52,]	911.46829	911.48475	911.49773	911.46998	911.43589
[53,]	952.40475	951.85585	951.83765	952.24540	952.39766
[54,]	1007.42668	1007.41415	1007.95004	1007.42758	1007.38508
[55,]	1054.11776	1054.89923	1054.10224	1054.44394	1054.79159
[56,]	1113.96599	1113.95926	1113.96968	1113.95371	1113.94464
[57,]	1156.98654	1156.93427	1159.00238	1157.03444	1158.92111
[58,]	1187.83263	1187.69251	1187.68199	1187.68081	1187.91383
[59,]	1242.30081	1239.65328	1239.66389	1239.60043	1239.62384

> result<-rowMeans(xyz)

> result

[1]	2.0649	6.5928	10.0805	14.9690	19.1316	24.0101
[7]	28.2811	33.3570	38.8504	44.0149	49.9267	56.4550
[13]	63.2835	70.5646	77.9440	85.8587	93.4580	102.2056
[19]	110.5914	121.5071	131.3736	141.1410	152.6966	164.2171
[25]	175.9800	188.6443	201.1879	215.8383	231.2367	246.4471
[31]	263.3380	280.5683	297.9573	319.4248	341.2758	364.4672
[37]	389.0956	411.3404	438.2907	463.4767	485.5917	512.3731
[43]	534.8651	561.6373	594.4565	629.1097	667.5355	710.0640
[49]	750.5693	795.7116	858.9556	911.4713	952.1483	1007.5207
[55]	1054.4710	1113.9587	1157.7757	1187.7604	1240.1684

> resultdf<-data.frame(actualbnkwh=kwhgdp$bn_kwh, predbnkwh=result)

> resultdf

	actualbnkwh	predbnkwh
1	16.94	2.06
2	20.15	6.59
3	23.36	10.08
4	26.57	14.97
5	29.78	19.13
6	32.99	24.01
7	37.81	28.28
8	42.62	33.36
9	47.43	38.85
10	51.62	44.01
11	55.80	49.93
12	59.43	56.45
13	63.06	63.28
14	66.69	70.56
15	72.94	77.94
16	79.20	85.86
17	85.30	93.46
18	91.40	102.21
19	102.52	110.59
20	104.70	121.51
21	120.80	131.37
22	122.10	141.14
23	130.30	152.70
24	140.20	164.22
25	156.86	175.98
26	170.40	188.64
27	187.70	201.19
28	202.10	215.84
29	221.40	231.24
30	245.44	246.45
31	264.30	263.34
32	287.03	280.57
33	301.40	297.96
34	324.00	319.42
35	350.40	341.28
36	380.00	364.47
37	395.89	389.10
38	421.70	411.34
39	448.50	438.29
40	480.70	463.48
41	499.50	485.59
42	517.44	512.37
43	532.70	534.87
44	565.10	561.64
45	594.40	594.46
46	623.80	629.11
47	670.65	667.54
48	723.00	710.06
49	741.20	750.57
50	799.80	795.71
51	844.80	858.96
52	923.20	911.47
53	964.50	952.15
54	1014.80	1007.52
55	1048.40	1054.47
56	1090.85	1113.96
57	1135.33	1157.78
58	1206.31	1187.76
59	1249.34	1240.17

Figure 4 actual bnkwh versus predicted bnkwh

> plot(resultdf$actualbnkwh, resultdf$predbnkwh, pch=16, col=4, xlab="actual bnkwh", ylab="predicted bnkwh", main="Leave-one-out cross validation")

> abline(0,1,col=2)

> rmse<-sqrt(sum((resultdf$actualbnkwh-resultdf$predbnkwh)^2)/nrow(resultdf))

> rmse

[1] 11.74785

The author can be reached at: arg1962@gmail.com    mobile: 9488361726